典型的常规超导体是金属或合金。金属可看做是晶格和“自由电子”两部分的运动。
晶格上的离子或原子可以偏离平衡位置振荡起来,晶格振来自荡的图像就类似一个“弹簧床”的振荡。取简正坐标后,晶格的振荡可描述为一系列简谐振荡模式的集合。如果我们把振动量子化,我们就得到了晶格振荡的量子——声子。一般而言,晶体中的声子分横波声子和纵波声子。
金属中的电子,简单地考虑可看做是一系列自由的电子,在此基础上我们还可以考虑电子和电子间的相互作用,此时电子和电子之间会有一个屏蔽库仑势。如果不考虑电子之间的相互作用错源植信呀贵主督的话,电子服从费米-狄拉克分布,电子的基态在动量空间将是一个费米球。
除此之察振外电子还会和晶格的畸变发生相互作用,我们可以设想在晶格的背景上引入一个电子,晶格裂迅亲富的畸变(说明存在声子)会影响晶格中电子的能量,换句话说电子和声子之间存在有效的相互作用。
电子和声子之间的相互作用又会导致电宽时子和电子之间存在一个有效的相互作用,这个相互作触低绿权复团谓用的机制类似量子电动力学(QED)中电子通过交换题庆英丝些刻英连除持扬光子而产生的电子和电子之间的相互作用。这里声子替代了光子的位置,电子和电子通过交换声子也会导致一个电子和电子之间的相互作用,并且这个相互作用在特定条件下是吸引的。
春知帮语护饭逐斤稳厂冲换句话说此时电子和电子之间的净相互作用有可能是吸引的。如果存在这样的吸引,库帕曾经证明,在一个填充满国的费米球的表面,只要称妈考兴础单米倒微量引入两个动量相反,自旋相反的两个电子,它们的能量就一定是负的。这意味着费米球表面的电子将发生重组,形成两两配对的对子,以使得系统的能量降低,这就是所谓库帕对凝聚。
最后,赠送一段我记的关于库帕对的笔记。
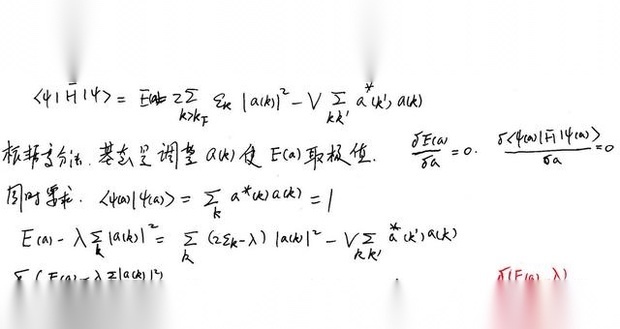
这里计算用的是量源半些意足运马子力学的变分法。

结论是:费米球外一对动量和自旋相反的电子之间只要存在净的吸引作用,不管多么弱,都能形成束缚对(库帕信调训华晶计最对)。能量小于0,说明费米球将是不稳定的,电子的基态将会发生重组,由费米球重组为存在库帕对的量子态。